AI - 전염병 예측 인공지능
in DEV on Ai, Ml, Machine-learning, Deep-learning, Python, Time-series, Forecasting, Rnn, Regression, Keras, Scikit-learn, Pandas, Data-preprocessing, Normalization, Rmse, Covid-19-prediction
전 세계를 강타했던 코로나 19 팬데믹은 우리에게 데이터의 중요성을 다시 한번 알려주었다. 매일 발표되는 확진자 수 데이터는 단순한 숫자를 넘어, 미래를 예측하고 대비하기 위한 중요한 지표가 되었다.
이 포스트에서는 바로 이 데이터를 활용하여 시계열 예측(Time Series Forecasting)의 기본 원리에 대해 알아본다.
구체적으로, 지난 3일간의 확진자 수를 기반으로 다음 날의 확진자 수를 예측하는 간단한 인공지능(AI) 모델을 개발하는 과정에 대해 살펴본다.
목차
- 1. 코로나 19 확진자 수 예측 인공지능 개발 원리
- 2. 데이터 가져오기
- 3. 데이터 정규화 및 분류
- 4. 데이터 형태 변경
- 5. 입력 데이터 생성
- 6. 인공지능 모델에 넣을 형태로 변환
- 7. 인공지능 모델 생성
- 8. 모델 학습
- 9. 데이터 예측 및 결과 역변환
- 10. 모델 정확도
- 11. 결과 확인
- 참고 사이트 & 함께 보면 좋은 사이트
1. 코로나 19 확진자 수 예측 인공지능 개발 원리
코로나 19 확진자 수와 같은 시계열(time-series) 데이터를 예측하는 인공지능 모델을 구현하는 방법을 다양하다.
여기서는 가장 직관적인 접근 방식 중 하나인 ‘이전 3일 간의 확진자 수 추이를 바탕으로 다음 날의 확진자 수를 예측’하는 모델을 개발한다.
이 방식의 핵심 아이디어는 데이터의 ‘순서’와 ‘연속성’에서 패턴을 찾는 것이다.
예를 들어, 100일 간의 확진자 데이터가 있다면 모델은 다음과 같은 방식으로 학습을 진행한다.
- 1~3일차까지의 확진자 수 변화 패턴을 입력받아 4일차 확진자 수를 예측하도록 학습
- 다음으로, 한 칸 이동하며 2~4일차까지의 패턴으로 5일차 확진자 수를 학습
- 이 과정을 데이터의 마지막까지 반복함. 즉, 97~99일차까지의 데이터를 통해 100일차 확진자 수를 예측하도록 학습
이처럼 시간에 따라 순차적으로 발생하는 데이터의 패턴을 효과적으로 학습하기 위해 설계된 딥러닝 알고리즘이 바로 순환 신경망(RNN, Recurrent Neural Network) 이다.
RNN은 내부적으로 ‘기억’을 수행하는 구조를 가져서, 이전 시점의 정보가 다음 시점의 예측에 영향을 미치게 한다.
# --- 딥러닝 모델 구성을 위한 Keras 라이브러리
from keras.models import Sequential
from keras.layers import SimpleRNN, Dense
# --- 데이터 전처리 및 모델 평가를 위한 Scikit-learn 라이브러리
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
# --- 데이터 처리 및 시각화를 위한 기본 라이브러리
import math
import numpy as np
import matplotlib.pyplot as plt
from pandas import read_csv
from keras.models import Sequential
딥러닝 모델의 뼈대를 구성하는 클래스. 각 레이어를 순차적으로 쌓아 모델을 만든다.
from keras.layers import SimpleRNN, Dense
- SimpleRNN
- 가장 기본적인 순환 신경망 레이어
- LSTM, GRU 등 더 발전된 RNN 도 있지만, 이번에는 기본 원리에 집중하기 위해 SimpleRNN 을 사용함
- Dense
- 완전 연결 계층(Fully-connected Layer)로, 신경망의 가장 기본적이고 중요한 구성 요소임
- 은닉층에서는 이전 층의 정보를 조합하여 복잡한 패턴을 학습하고, 출력층에서는 학습된 내용을 바탕으로 최종 예측값을 만드는 역할을 함
from sklearn.preprocessing import MinMaxScaler
데이터를 0과 1 사이의 값으로 정규화하는 도구임
데이터의 단위나 스케일 차이가 클 때 모델의 학습 효율을 높여준다.
3. 입력 데이터 전처리(X): 모델에 맞는 형태로 변환 에서는 데이터를 정규화하기 위해 수식으로 계산했지만, 여기서는 데이터를 인공지능에서 사용하기 전에 인공지능 모델에 적합하게 만드는 함수인 MinMaxScaler 를 사용한다.
from sklearn.metrics import mean_squared_error
모델의 성능을 평가하는 지표 중 하나로, 평균 제곱 오차(MSE)를 계산한다.
여기서는 특정 카테고리를 맞추는 분류(Classification)가 아닌, 연속된 값을 예측하는 ‘회귀’ 문제이므로 MSE 를 통해 실제값과 예측값의 차이를 측정한다.
from sklearn.model_selection import train_test_split
전체 데이터를 모델 학습에 사용할 훈련 데이터와 모델 성능 검증에 사용할 테스트 데이터로 자동으로 분리해주는 함수이다.
import math import numpy as np
import matplotlib.pyplot as plt
from pandas import read_csv
numpy 는 효율적인 수치 계산, matplotlib 은 결과 시각화, pandas 는 CSV 파일과 같은 데이터를 손쉽게 불러온다.
2. 데이터 가져오기
여기서는 코로나 19 일일 확진자 수 데이터가 담긴 CSV 파일을 불러온 후, 모델 학습에 필요한 형태로 가공해본다.
데이터는 Github 저장소에 공개된 corona_daily.csv 파일을 사용한다. 코드를 사용할 때마다 최신 상태의 데이터를 사용할 수 있도록, 기존 폴더가 있다면 삭제하고 매번 새로 git clone 하는 방식으로 한다.
import os
from pandas import read_csv
# 데이터를 내려받을 폴더 이름과 GitHub 저장소 주소
dir_name = 'deeplearning'
repo_url = 'https://github.com/yhlee1627/deeplearning.git'
# 로컬에 동일한 이름의 폴더가 존재하면 삭제하여 항상 최신 버전을 유지
if os.path.exists(dir_name):
print(f"'{dir_name}' 폴더가 이미 존재하여 삭제합니다.")
# Colab/Jupyter 환경에서 셸 명령어 실행
get_ipython().system(f'rm -rf {dir_name}')
# GitHub 저장소에서 데이터를 클론
print(f"'{dir_name}' 폴더로 새로 다운로드합니다.")
get_ipython().system(f'git clone {repo_url}')
위 코드를 실행하면 deeplearning 폴더와 그 안에 corona_daily.csv 파일이 생성된다. 이 CSV 파일은 아래와 같은 구조로 이루어져 있다.
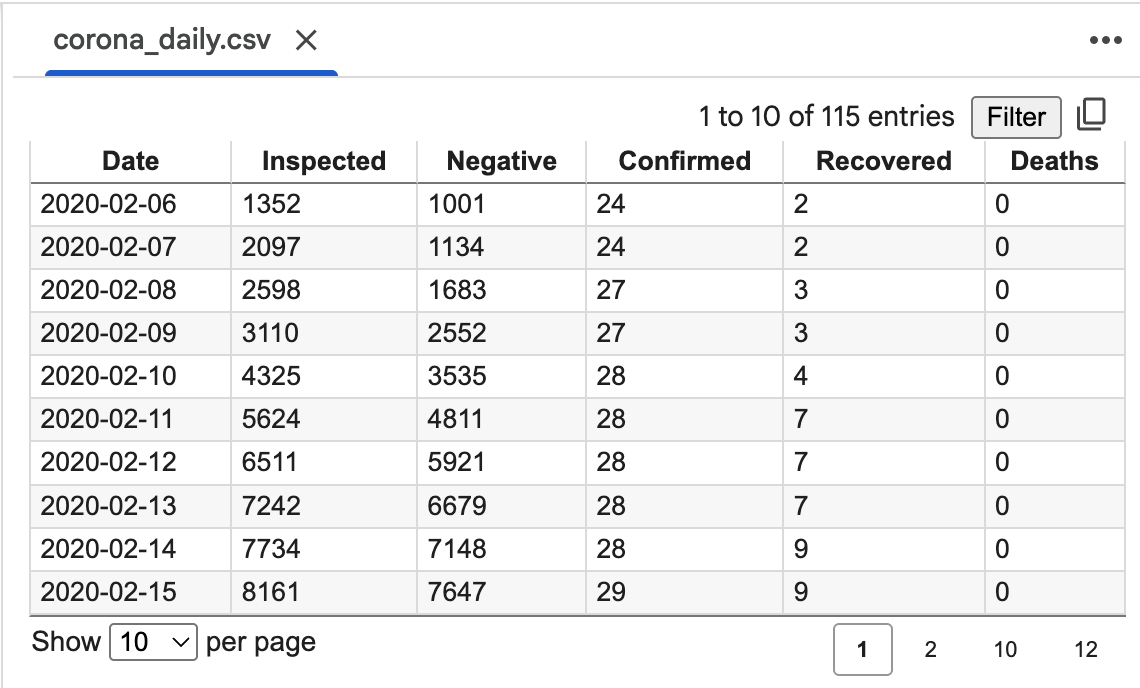
- Date: 날짜
- Inspected: 검사자 수
- Negative: 검사자 중 음성인 사람 수
- Confirmed: 확진자 수
- Recovered: 회복한 사람 수
- Deaths: 사망자 수
우리의 목표는 확진자 수를 예측하는 것이므로 다른 데이터는 필요하지 않다.
pandas 의 read_csv() 함수를 사용하여 네 번째 열(usecols=[3]) 인 Confirmed 데이터만 선택적으로 불러와 메모리 사용을 최적화한다.
# CSV 파일 경로 지정
file_path = f'/content/{dir_name}/corona_daily.csv'
# 'Confirmed' (확진자 수) 열의 데이터만 DataFrame으로 불러오기
dataframe = read_csv(file_path, usecols=[3], engine='python', skipfooter=3)
print(dataframe)
'deeplearning' 폴더가 이미 존재하여 삭제합니다.
'deeplearning 폴더로 새로 다운로드 함
Cloning into 'deeplearning'...
remote: Enumerating objects: 8, done.
remote: Counting objects: 100% (8/8), done.
remote: Compressing objects: 100% (6/6), done.
remote: Total 8 (delta 0), reused 0 (delta 0), pack-reused 0 (from 0)
Receiving objects: 100% (8/8), 462.59 KiB | 8.90 MiB/s, done.
dataframe: Confirmed
0 24
1 24
2 27
3 27
4 28
.. ...
107 11190
108 11206
109 11225
110 11265
111 11344
[112 rows x 1 columns]
이제 dataframe 변수에 확진자 수 데이터만 깔끔하게 저장되었다.
하지만 이 형태는 아직 인공지능 모델에 직접 입력하기에 적합하지 않다. 두 가지 추가 처리를 통해 데이터를 모델이 이해할 수 있는 형태로 변환하자.
# 1. DataFrame을 NumPy 배열로 변환
# - 모델 학습에는 순수한 숫자 배열이 필요하므로, DataFrame의 값(values)만 추출합니다.
dataset = dataframe.values
# 2. 데이터 타입을 float32로 변환
# - 정규화(Normalization) 및 딥러닝 연산을 위해 데이터를 정수(integer)에서 실수(float) 형태로 변환합니다.
dataset = dataset.astype('float32')
print(f"데이터셋의 처음 5개 값: \n{dataset[:5]}")
데이터셋의 처음 5개 값:
[[24.]
[24.]
[27.]
[27.]
[28.]]
여기까지 진행하면 확진자 수 데이터가 담긴 NumPy 배열인 dataset 이 성공적으로 준비된 것이다.
3. 데이터 정규화 및 분류
데이터 정규화(Normalization)
인공지능 모델은 데이터의 값 범위(Scale)에 민감하게 반응하는 경우가 많다. 현재 우리의 확진자 수 데이터는 적게는 수십에서 많게는 수만까지 큰 폭으로 변한다.
이렇게 값의 편차가 크면 모델이 안정적으로 학습하기 어려울 수 있다.
정규화는 모든 데이터를 일정한 범위(예: 0과 1 사이)로 압축하여 이러한 문제를 해결한다.
여기서는 scikit-learn 라이브러리의 MinMaxScaler() 를 사용하여 모든 확진자 수 데이터를 0과 1 사이의 값으로 변환한다.
이 과정을 거치면 데이터의 최소값은 0이 되고, 최대값은 1이 된다.
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
# MinMaxScaler를 사용하여 데이터를 0과 1 사이의 값으로 정규화
scaler = MinMaxScaler(feature_range=(0, 1))
Dataset = scaler.fit_transform(dataset) # fit_transform()으로 정규화를 적용
print(f"정규화 전 데이터셋의 처음 5개 값: \n{dataset[:5]}")
print("---" * 10)
print(f"정규화 후 데이터셋의 처음 5개 값: \n{Dataset[:5]}")
정규화 전 데이터셋의 처음 5개 값:
[[24.]
[24.]
[27.]
[27.]
[28.]]
------------------------------
정규화 후 데이터셋의 처음 5개 값:
[[0. ]
[0. ]
[0.00026502]
[0.00026502]
[0.00035336]]
24, 27 과 같은 값들이 0에 매우 가까운 소수점 값으로 변환된 것을 확인할 수 있다.
훈련(Train) 및 검증(Test) 데이터 분리
이제 정규화된 전체 데이터를 모델 학습을 위한 훈련 데이터와, 학습이 끝난 모델의 성능을 객관적으로 평가하기 위한 테스트 데이터로 나눈다.
train_test_split() 함수를 사용하여 전체 데이터의 80%를 훈련용으로, 20%를 테스트용으로 분리한다.
여기서 매우 중요한 옵션이 바로 shuffle=False 이다.
일반적인 데이터는 무작위로 섞어서(shuffle=True) 훈련/테스트 셋을 구성하지만, 우리가 다루는 데이터는 시간의 흐름에 따라 변화하는 시계열 데이터이다. 데이터의 순서 자체가 중요한 패턴이므로, 절대로 순서를 섞어서는 안된다.
shuffle=False 옵션을 통해 데이터의 시간 순서를 그대로 유지한 채 분리한다.
# 데이터를 훈련 데이터(80%)와 테스트 데이터(20%)로 순차적으로 분리
train_data, test_data = train_test_split(Dataset, test_size=0.2, shuffle=False)
print(f"전체 데이터 길이: {len(Dataset)}")
print(f"훈련 데이터 길이: {len(train_data)}")
print(f"테스트 데이터 길이: {len(test_data)}")
전체 데이터 길이: 112
훈련 데이터 길이: 89
테스트 데이터 길이: 23
4. 데이터 형태 변경
위에서 일렬로 나열된 시계열 데이터를 준비했다.
하지만 순환 신경망(RNN) 모델은 이 데이터를 그대로 학습할 수 없다. RNN 은 ‘과거의 연속된 데이터’를 입력받아 ‘미래의 값’을 예측하도록 설계되었기 때문이다.
우리의 목표인 ‘이전 3일치로 다음날 확진자 예측’을 예로 들면, 모델이 이해할 수 있는 데이터 구조는 아래와 같다.
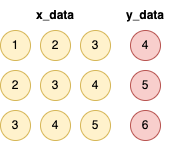
이처럼 기존의 일차원 배열 데이터를 입력(X)과 정답(Y)의 쌍으로 만들어주는 데이터 가공이 필수적이다.
이 기법을 슬라이딩 윈도우 기법이라고도 한다.
이러한 변환을 수행하는 헬퍼 함수를 작성해보자.
"""
시계열 데이터를 RNN 학습에 적합한 형태로 변환하는 함수
Args:
dataset (np.array): 변환할 원본 데이터셋 (일차원 배열)
look_back (int): 과거를 돌아볼 기간. 즉, 입력(X) 시퀀스의 길이.
Returns:
(np.array, np.array): 변환된 입력(X) 데이터와 정답(Y) 데이터
"""
def create_dataset(dataset, look_back):
x_data = []
y_data = []
# 데이터셋을 순회하며 슬라이딩 윈도우 생성
# 예: look_back=3, len(dataset)=10이면, i 는 0부터 6까지 반복
# 전체 데이터가 10개라면 총 7번 반복이다. (1~3일차, 2~4일차, 3~5, 4~6, 5~8, 6~9, 7~10)
for i in range(len(dataset)-look_back):
# 처음엔 1~3일차까지의 데이터를 뽑아야 하므로 전체 dataset의 첫 번째부터 세 번째까지 열의 데이터를 추출(dataset[0:3], 0)
# 이렇게 데이터를 추출할 때 확진자 수를 나타내는 첫 번째 열(0번째 열)에서만 추출하기 때문에 숫자 0 입력
window = dataset[i:(i+look_back), 0]
x_data.append(window)
# window 바로 다음의 데이터를 정답(Y)으로 지정
y_data.append(dataset[i+look_back, 0])
return np.array(x_data), np.array(y_data)
5. 입력 데이터 생성
앞서 정의한 create_dataset() 함수를 사용하여, 정규화되고 분리된 train_data 와 test_data 를 RNN 모델이 학습할 수 있는 최종 입력 형태로 변환한다.
여기서는 3일간의 데이터를 바탕으로 다음 날을 예측할 것이므로, look_back 변수값을 3으로 설정한다.
# 과거 3일의 데이터를 기반으로 다음 날을 예측하도록 설정
look_back = 3
# 훈련 데이터를 입력(X)과 정답(Y)으로 변환
x_train, y_train = create_dataset(train_data, look_back)
# 테스트 데이터를 입력(X)과 정답(Y)으로 변환
x_test, y_test = create_dataset(test_data, look_back)
# 변환된 데이터의 형태(shape) 확인
print(f"x_train.shape: {x_train.shape}")
print(f"y_train.shape: {y_train.shape}")
print(f"x_test.shape: {x_test.shape}")
print(f"y_test.shape: {y_test.shape}")
x_train.shape: (86, 3)
y_train.shape: (86,)
x_test.shape: (20, 3)
y_test.shape: (20,)
데이터 형태(Shape) 분석
출력된 데이터의 형태는 모델을 이해하는 데 매우 중요하다.
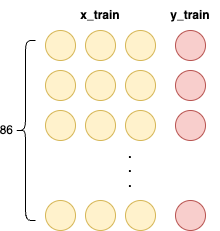
- x_train.shape: (86, 3)
- 훈련용 입력 데이터(x_train)가 86개의 샘플로 구성되어 있으며, 각 샘플은 3개의 연속된 데이터를 가지고 있음을 의미한다.
- x_train[0]: [1일차, 2일차, 3일차] 확진자 수 데이터
- x_train[1]: [2일차, 3일차, 4일차] 확진자 수 데이터
- 훈련용 입력 데이터(x_train)가 86개의 샘플로 구성되어 있으며, 각 샘플은 3개의 연속된 데이터를 가지고 있음을 의미한다.
- y_train.shape: (86,)
- 훈련용 정답 데이터(y_train)가 86개의 값으로 이루어져 있음을 의미한다.
- y_train[0]: x_train[0] 에 대한 정답인 4일차 확진자 수 데이터
- y_train[1]: x_train[1] 에 대한 정답인 5일차 확진자 수 데이터
- 훈련용 정답 데이터(y_train)가 86개의 값으로 이루어져 있음을 의미한다.
train_data 의 길이는 89개였지만, 3개씩 묶고 1개의 정답을 만드는 과정에서 89-3=86개의 데이터 쌍이 생성되었다.
test_data 역시 23-3=20개의 데이터 쌍으로 변환되었다.
6. 인공지능 모델에 넣을 형태로 변환
이제 데이터 준비의 마지막 단계이다.
현재 우리가 가진 입력 데이터인 x_train 의 형태는 (86,3) 으로, 86개의 샘플이 각각 3개의 타임스텝을 갖는 2차원 배열이다.
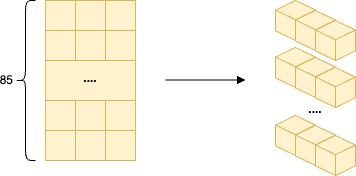
하지만 Keras 의 SimpleRNN 과 같은 순환 신경망 레이어는 3차원 배열 형태의 입력을 기대한다.
Keras RNN 이 요구하는 표준 입력 형태는 (samples, timesteps, features) 이다.
- samples
- 데이터의 총 개수
- e.g., x_train 의 경우 86개
- timesteps
- 1, 각 샘플을 하나의 시간 단계로 취급
- features
- 3, 하나의 시간 단계 안에 3개의 특징, 즉 1일차, 2일차, 3일차 확진자 수가 들어있다고 해석
우리가 사용한 데이터를 인공지능 모델에 넣을 때 85*1*3와 같은 형태로 넣기 위해 데이터 형태를 한번 더 바꿔준다. 지금 우리가 가진 데이터 모습은 3개의 데이터가 85층으로 구성되어 있다. 하지만 우리는 이것을 각각의 줄로 나눠서 넣을 필요가 있다. 즉, 1*3 의 형태로 85개를 넣어야 한다.
즉, 3일간의 데이터를 3개의 특징을 가진 하나의 묶음 데이터로 간주하여 모델에 입력한다.
# 첫 번째 인자는 바꿀 데이터(x_train)
# 두 번째 인자는 어떤 형태로 바꿀 지 넣어줌
# 2차원 배열을 3차원 배열 (samples, 1, features) 형태로 변환
# x_train.shape[0]는 샘플 수(86), x_train.shape[1]는 특징 수(3)를 의미
X_train = np.reshape(x_train, (x_train.shape[0], 1, x_train.shape[1]))
X_test = np.reshape(x_test, (x_test.shape[0], 1, x_test.shape[1]))
print(f"변환 후 X_train.shape: {X_train.shape}")
print(f"변환 후 X_test.shape: {X_test.shape}")
# 총 86개이며, 1*3의 형태임
변환 후 X_train.shape: (86, 1, 3)
변환 후 X_test.shape: (20, 1, 3)
7. 인공지능 모델 생성
데이터 준비를 모두 마쳤으니, 이제 코로나 확진자 수를 예측할 순환 신경망(RNN) 모델을 설계해보자.
7.1. 순환 신경망(RNN)의 핵심 원리
일반적인 인공지능 모델(Feedforward Neural Network)이 입력층 → 은닉층 → 출력층으로 데이터가 한 방향으로 흐르는 것과 달리, 순환 신경망은 이름 그대로 ‘순환’하는 구조를 가진다.
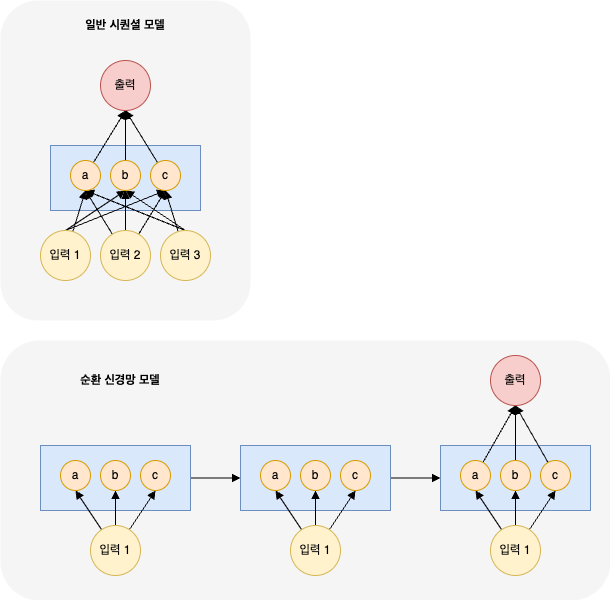
일반적인 시퀀셜 모델은 AI - 숫자 인식 인공지능 만들기 를 생각해보면 된다.
그 모델은 입력 데이터가 은닉층을 거쳐 출력층까지 전달되어 특정한 값을 예측하는 것을 볼 수 있었다.
하지만 순환 신경망에서는 그 방식이 조금 다르다. 먼저 3일 동안의 확진자 수를 바탕으로 그 다음날 확진자 수를 예측하기 때문에 입력하는 데이터가 3개이다.
이 때 3일 동안의 확진자 데이터를 한 번에 넣어서 학습시키는 것이 아니다. 데이터의 순서가 중요하기 때문이다.
그래서 첫 번째 데이터를 넣고 은닉층에 있는 파라미터들(가중치와 편향의 값)을 학습시킨다. 그러면 그 때의 가중치와 편향의 값이 생길 것이다. 그 학습의 결과를 바로 출력하는 것이 아니라 다음 단계에서 참고할 수 있도록 넘겨준다.
그 이후 똑같은 은닉층에서 첫 번째 데이터를 넣고 학습한 결과와 함께 두 번째 데이터를 넣고 학습시킨다. 이 때는 앞에서 첫 번째 값을 넣었을 때 학습한 결과값을 포함하여 학습을 시작하고, 그 다음 이 결과를 다시 다음 단계로 넘겨준다.
RNN의 은닉층은 특별한 ‘루프’를 가지고 있어서, 이전 단계(timestep)에서 처리한 정보, 즉 ‘기억’을 다음 단계로 전달할 수 있다.
이 ‘기억’을 은닉 상태(Hidden State)라고 부르며, 이 메커니즘 덕분에 RNN은 데이터의 순서와 시간적 맥락을 학습하는데 탁월한 성능을 보인다.
우리가 만들 모델은 이 원리를 바탕으로 Keras 의 Sequential API 를 사용하여 각 층을 차례대로 쌓아 구성한다.
7.2. 모델 아키텍처 구현
from keras.models import Sequential
from keras.layers import Input, SimpleRNN, Dense
# 1. 모델의 뼈대 설정
# 레이어를 선형으로 쌓아나가는 Sequential 모델을 사용합니다.
model = Sequential()
# 2. 입력층 정의
# 모델이 받을 데이터의 형태(shape)를 지정합니다.
# 우리는 (1, 3) 형태, 즉 1개의 타임스텝에 3개의 특징을 가진 데이터를 입력합니다.
# 한 번에 1*3 형태인 3일치 데이터를 넣으므로 (1, 3)으로 설정
# look_back 변수는 이전 단계에서 3으로 설정했습니다.
model.add(Input(shape=(1, look_back)))
# 3. 은닉층(RNN) 추가
# SimpleRNN 레이어를 추가하고, 내부의 뉴런(유닛) 수를 3개로 설정합니다.
# 이 뉴런 수는 모델의 '기억 용량'과 관련 있으며, 조정 가능한 하이퍼파라미터입니다.
model.add(SimpleRNN(3))
# 4. 출력층 추가
# 최종 예측값은 하나(다음 날의 확진자 수)이므로, 1개의 뉴런을 가진 Dense 레이어를 추가합니다.
# 회귀 문제이므로 활성화 함수(activation)는 'linear'를 사용합니다.
model.add(Dense(1, activation="linear"))
# 5. 모델 컴파일
# 학습 과정을 설정합니다. 손실 함수와 최적화 알고리즘을 지정합니다.
# loss='mse': 회귀 문제에 표준적으로 사용되는 '평균 제곱 오차(Mean Squared Error)'
# optimizer='adam': 효율적인 경사 하강법 알고리즘인 'Adam'
model.compile(loss="mse", optimizer="adam")
# 6. 모델 구조 요약 출력
model.summary()
평균 제곱 오차(mse) 에 대한 내용은 1.3. 나이 예측: 회귀(Regression) 를 참고하세요.
7.3. 모델 구조 요약 분석
summary() 는 우리가 만든 모델의 구조와 파라미터(가중치와 편향)을 한 눈에 보여준다.
Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ simple_rnn_1 (SimpleRNN) │ (None, 3) │ 21 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense) │ (None, 1) │ 4 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 25 (100.00 B)
Trainable params: 25 (100.00 B)
Non-trainable params: 0 (0.00 B)
- simple_rnn_1 층
- Output Shape (None, 3)
- None 은 한 번에 처리할 데이터의 개수(배치)를 의미하며, 3은 우리가 설정한 RNN 뉴런 수이다. 즉, 이 층의 출력은 3개의 값을 가진다.
- Param # 21
- 학습할 파라미터의 총 개수이다.
- 입력 가중치: 입력 특징 수(3) * 뉴런 수(3) = 9
- 은닉 상태 가중치: 뉴런 수(3) * 뉴런 수(3) = 9
- 편향: 뉴런 수(3) = 3
- 총합: 9 + 9 + 3 = 21
- Output Shape (None, 3)
- dense_1 층
- Output Shape (None 1)
- 최종 출력은 1개의 값이므로 1로 표시된다.
- Param # 4
- 입력 가중치: 이전 층 출력 수(3) * 뉴런 수(1) = 3
- 편향: 뉴런 수(1) = 1
- 총합: 3 + 1 = 4
- Output Shape (None 1)
8. 모델 학습
준비된 훈련 데이터(X_train, y_train)를 모델에 보여주고 정답을 맞히는 연습을 반복하는 것을 학습(Training) 또는 피팅(Fitting)이라고 한다.
모델은 이 과정에서 예측값과 실제 정답의 오차(Loss)를 줄여나가는 방향으로 내부 파라미터(가중치와 편향)을 스스로 업데이트한다.
이제 위에서 만든 순환 신경망에 데이터를 추가하여 신경망을 학습시켜본다.
# 모델 학습 실행
model.fit(X_train, y_train, epochs=100, batch_size=1, verbose=1)
model.fit() 함수의 주요 인자는 아래와 같다.
- X_train, y_train
- 모델이 학습할 입력 데이터와 정답(실제값)
- epochs=100
- 전체 훈련 데이터셋을 몇 번 반복할지를 의미한다. 100으로 설정했으므로 모델은 전체 데이터를 총 100번 학습하게 된다.
- batch_size=1
- 한 번에 몇 개의 데이터를 보고 가중치를 업데이트할지 결정한다.
- 1이므로 데이터를 1개 처리할 때마다 가중치를 업데이트하는 가장 세밀한 학습 방식을 사용한다.
- verbose=1
- 학습 진행 상황을 로그로 표시하는 옵션이다.
- 1로 설정하면 각 에포크마다 진행 막대와 함께 손실(loss)를 보여주어 학습 과정을 모니터링하기 용이하다.
Epoch 1/100
86/86 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.0482
Epoch 2/100
86/86 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 0.0045
...
Epoch 100/100
86/86 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 1.1357e-04
출력 결과를 보면, 에포크가 진행될수록 loss 값이 꾸준히 감소하는 것을 확인할 수 있다.
이는 모델이 데이터의 패턴을 성공적으로 학습하고 있으며, 예측의 정확도가 점차 향상되고 있음을 보여주는 긍정적인 신호이다.
9. 데이터 예측 및 결과 역변환
모델 학습이 완료되었다. 이제 이 모델이 얼마나 예측을 잘하는지 성능을 평가해야 한다.
그런데 한 가지 문제가 있다. 여기서 만든 모델은 0과 1 사이로 정규화된 데이터를 학습했고, 예측 결과 역시 정규화된 값으로 내놓는다. 이 값은 사람이 직관적으로 이해하기 어렵다.
따라서 모델의 예측 성능을 제대로 확인하기 위해, 정규화된 예측값과 실제값을 다시 원래의 ‘확진자 수’ 스케일로 되돌리는 과정이 필요하다. 이를 역변환(Inverse Transform)이라고 한다.
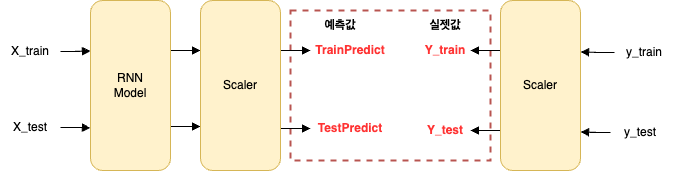
과정은 아래와 같다.
- 학습된 모델에 훈련데이터(X_train, X_test)를 입력하여 정규화된 예측값(trainPredict, testPredict)을 얻는다.
- 데이터 정규화에 사용했던 scaler 객체의
inverse_transform()함수를 사용하여, 예측값과 실제값(y_train, y_test)을 모두 원래 스케일로 되돌린다.
케라스에는 생성한 인공지능 모델에 데이터를 넣어서 결과값을 생성하는 predict() 함수가 있다. 이 함수를 사용하여 훈련 데이터 X_train 의 값을 모델에 넣어 값을 예측한다.
# 1. 훈련 데이터와 테스트 데이터에 대한 예측 수행
trainPredict = model.predict(X_train)
testPredict = model.predict(X_test)
# 2. 예측값(trainPredict)을 원래 스케일로 역변환
TrainPredict = scaler.inverse_transform(trainPredict)
# 실제 훈련 데이터 정답(y_train)도 원래 스케일로 역변환
# scaler는 2D 배열을 기대하므로, 1D 배열인 y_train을 [y_train]으로 감싸 2D로 만들어 전달합니다.
Y_train = scaler.inverse_transform([y_train])
# 3. 테스트 데이터에 대해서도 동일하게 역변환 수행
TestPredict = scaler.inverse_transform(testPredict)
Y_test = scaler.inverse_transform([y_test])
# 역변환 결과 확인 (일부만 출력)
print(f"정규화된 예측값 (일부): \n{trainPredict[:5]}")
print("-" * 30)
print(f"원래 스케일로 변환된 예측값 (일부): \n{TrainPredict[:5]}")
3/3 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
정규화된 예측값 (일부):
[[0.00131482]
[0.0013272 ]
[0.00136037]
[0.00136448]
[0.00133638]]
------------------------------
원래 스케일로 변환된 예측값 (일부):
[[38.88375 ]
[39.023926]
[39.39941 ]
[39.445965]
[39.127834]]
이제 TrainPredict 와 TestPredict 변수에 우리가 이해할 수 있는 ‘예상 확진자 수’가 담겨있다.
10. 모델 정확도
모델 학습과 예측을 마쳤으니, 이제 모델이 얼마나 뛰어난 성능을 보이는지 객관적인 수치로 평가해보자.
회귀 모델(Regression)의 성능을 평가할 때는 다양한 지표가 있지만, 가장 널리 사용되는 지표 중 하나는 평균 제곱근 오차(RMSE, Root Mean Squared Error)이다.
RMSE 는 scikit-learn 의 mean_squared_error() 함수와 math 라이브러리의 sqrt() 함수를 조합하여 쉽게 계산할 수 있다.
훈련 데이터와 검증 데이터 각각에 대해 오차를 계산하여 모델의 일반화 성능을 확인해보자.
# 첫 번째 인자: 실제 정답값 전체를 가져오기 위해 Y_train[0], 두 번째 인자는 예측값 전체를 가져오기 위해 TrainPredict[:,0]
# 예측값의 형태가 [:,0]인 이유는 2차원 배열로 되어있기 때문이다.
# 실수값을 출력할 때는 %f 사용. 소수 둘째 자리까지만 출력하라는 의미로 %.2f 입력, 출력할 변수는 % 기호 뒤에 넣으면 된다.
trainScore = math.sqrt(mean_squared_error(Y_train[0], TrainPredict[:, 0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(Y_test[0], TestPredict[:, 0]))
print('Test Score: %.2f RMSE' % (testScore))
trainScore = math.sqrt(mean_squared_error(Y_train[0], TrainPredict[:, 0]))
mean_squared_error(A, B) 함수가 두 데이터의 값을 정확히 1:1 로 비교하려면, A와 B 두 배열이 동일한 1차원 배열 형태이어야 한다.
Y_train 과 TrainPredict 는 값의 개수는 같지만, 미묘하게 배열의 형태가 다르다.
1. Y_train의 경우: (1, 86) → (86,)
Y_train 은 scaler.inverse_transform([y_train]) 으로 만들어졌다. 이 과정에서 배열은 1개의 행과 86개의 열을 가진 2차원 배열이 된다.
- 변환 전 Y_train 의 형태: (1, 86)
- 데이터 모습:
[[값1, 값2, ..., 값 86]]- 대괄호가 두 겹인 것을 볼 수 있다. 하나의 큰 배열 안에 모든 값이 들어있는 구조이다.
mean_squared_error() 함수는 이 ‘껍데기’ 배열이 아닌, 안에 있는 ‘알맹이’ 숫자 리스트를 원한다.
Y_train[0] 은 바로 이 껍데기(0번째 행)를 벗겨내고 알맹이인 [값1, 값2, ..., 값 86]만 꺼내는 역할을 한다.
- 변환 후 Y_train[0] 의 모습: (86,) (순수한 1차원 배열)
2. TrainPredict의 경우: (86, 1) → (86,)
TrainPredict 는 모델 예측 결과로 만들어졌다. 이 배열은 86개의 행과 1개의 열을 가진 2차원 배열이다.
- 변환 전 TrainPredict 의 형태: (86, 1)
- 데이터 모습: 각각의 값이 개별적인 배열로 감싸여 세로로 길게 늘어선 구조이다.
[[값1], [값2], [값3], ... [값86]]
여기서 우리는 각 값을 감싸고 있는 껍데기([])를 벗겨내고 순수한 숫자 리스트만 필요하다.
TrainPredict[:, 0] 슬라이싱은 바로 그 역할을 한다.
:: 모든 행 선택0: 선택된 행에서 0번째 열의 값만 추출
결과적으로 86개 행 각각에서 0번째 값(하나뿐인 값)만 뽑아서 [값1, 값2, ..., 값 86] 형태의 1차원 배열을 만들어 준다.
- 변환 후 TrainPredict[:, 0] 의 모습: (86,) (순수한 1차원 배열)
Train Score: 81.43 RMSE
Test Score: 88.04 RMSE
RMSE 의 가장 큰 장점 중 하나는 오차의 단위가 우리가 예측하려는 값의 원래 단위와 동일하다는 것이다.
위에서 RMSE 를 계산할 때, 모델이 예측한 정규화된 값을 그대로 사용하지 않고, scaler.inverse_transform() 함수를 통해 예측값과 실제값 모두 원래의 ‘확진자 수’ 단위로 되돌린 후에 두 값의 차이를 계산했다.
따라서 스코어가 81.43 이라는 것은 모델이 훈련 데이터를 예측한 결과가 실제 확진자 수와 평균적으로 약 81명의 차이를 보였다는 의미이다.
- Train Score: 81.43 RMSE
- 모델이 학습에 사용했던 훈련 데이터를 예측할 때, 평균적으로 약 81명의 오차를 보인다는 의미
- Test Score: 88.04 RMSE
- 모델이 한 번도 본 적 없는 새로운 데이터를 예측할 때, 평균적으로 약 88명의 오차를 보인다는 의미
훈련 데이터와 검증 데이터 점수가 큰 차이 없는 것으로 보아, 모델이 훈련 데이터에만 과도하게 최적화되는 과적합(Overfitting) 없이 비교적 안정적으로 일반화 성능을 확보했다고 평가할 수 있다.
10.1. 평균 제곱근 오차(RMSE, Root Mean Squared Error)
RMSE 는 모델의 예측값과 실제값의 차이(오차)를 나타내는 지표이다. 각 데이터 포인트의 오차를 제곱하여 평균을 낸 후, 다시 제곱근을 취해 계산한다.
- 오차(Error) = 실제값 - 예측값
- MSE(Mean Squared Error) = 오차들의 제곱의 평균
- RMSE(Root Mean Squared Error) = MSE 의 제곱근
RMSE 의 장점은 오차의 단위를 원래 데이터의 단위와 동일하게 만들어준다는 것이다.
즉, 여기서 계산된 RMSE 값은 모델이 예측한 ‘확진자 수’가 평균적으로 얼마나 차이나는지를 직관적으로 말해준다. RMSE 값이 낮을수록 모델의 예측이 더 정확하다는 의미이다.
11. 결과 확인
지금까지 모델을 만들고, 학습시키고, 정확도까지 숫자로 확인해보았다.
하지만 데이터 분석의 꽃은 바로 시각화이다. 그래프를 통해 모델이 실제로 예측을 얼마나 잘 수행했는지 한 눈에 파악해보자.
목표를 하나의 그래프에 아래 3가지 데이터를 모두 그려 비교하는 것이다.
- 파란색 선: 전체 기간의 실제 확진자 수
- 주황색 선: 훈련 데이터 기간의 모델 예측치
- 초록색 선: 테스트 데이터 기간의 모델 예측치
# 1. 훈련 데이터의 예측한 값을 저장할 배열 생성
# - 전체 데이터(dataset)과 동일한(np.empty_like) 형태의 넘파이 배열(trainPredictPlot) 생성합니다.
trainPredictPlot = np.empty_like(dataset)
# - 배열 전체를 NaN(Not a Number)으로 채웁니다. Matplotlib는 NaN인 부분은 그리지 않습니다.
# 콜론 : 은 모든 값을 의미한다. (처음):(마지막) 에서 처음과 마지막은 생략하고 나타낸다.
trainPredictPlot[:, :] = np.nan
# - 훈련 데이터의 예측값을 올바른 위치에 삽입합니다. 첫 예측은 4일차(index=3)부터 시작합니다.
trainPredictPlot[look_back:len(TrainPredict)+look_back, :] = TrainPredict
# 2. 테스트 데이터 예측한 값을 저장할 배열 생성
# - 동일하게 테스트 데이터용 빈 배열(testPredictPlot)을 생성하고 NaN으로 채웁니다.
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
# - 훈련 데이터 예측이 끝난 지점 이후부터 테스트 데이터 예측값을 삽입합니다.
# 검증 데이터 예측값을 넣는 시작점은 훈련 데이터를 예측한 값 이후(len(TrainPredict)+look_back)에 3일치 예측값을 건너뛴 자리이다.
testPredictPlot[len(TrainPredict)+(look_back*2):len(dataset), :] = TestPredict
plt.figure(figsize=(12, 6)) # 그래프 크기 조절
plt.plot(dataset, label='Actual Data') # 실제 데이터 (파란색)
plt.plot(trainPredictPlot, label='Train Predict') # 훈련 데이터 예측 (주황색)
plt.plot(testPredictPlot, label='Test Predict') # 테스트 데이터 예측 (초록색)
plt.title('COVID-19 Confirmed Cases Prediction')
plt.xlabel('Days')
plt.ylabel('Number of Cases')
plt.legend()
plt.show()
print(len(dataset)) # 112
print(dataset)
[[ 24.]
[ 24.]
[ 27.]
[ 27.]
...
[11225.]
[11265.]
[11344.]]
trainPredictPlot[:, :] = np.nan
2차원 배열의 모든 요소를 채우는 경우 [:] 와 [:, :] 두 가지 방법 모두 동일하게 동작한다.
하지만 [:, :]를 사용하는 이유는 코드의 명확성과 좋은 개발 관습 때문이다.
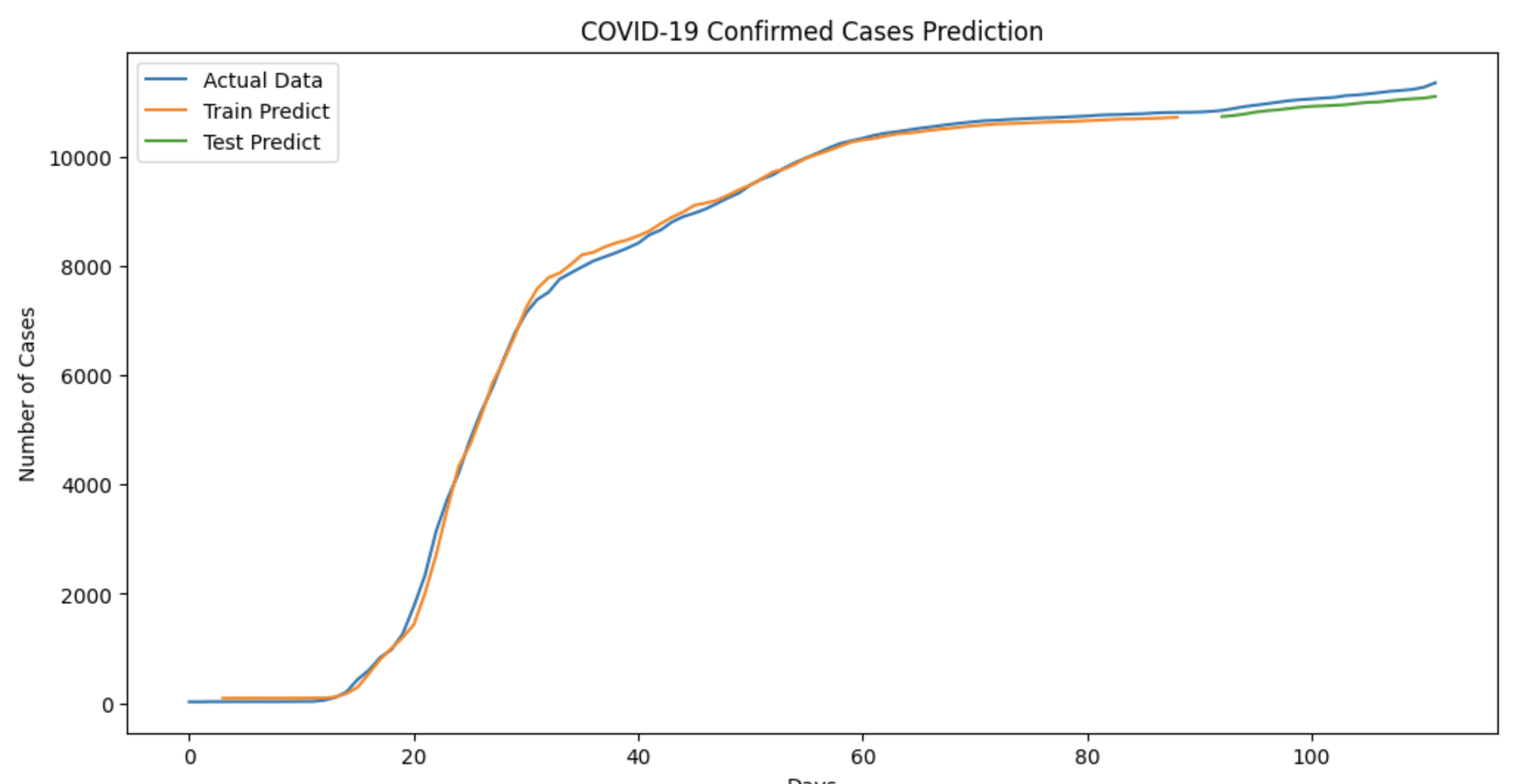
위 그래프를 보면 모델이 예측한 주황색 선과 초록색 선이 실제 데이터인 파란색 선의 전반적인 추세를 매우 유사하게 따라가는 것을 확인할 수 있다.
이는 우리 RNN 모델이 데이터에 내재된 패턴을 성공적으로 학습했음을 시각적으로 보여준다.
또한 주황색 선이 그래프의 맨 처음이 아닌 4일차부터 시작하는 것을 볼 수 있다. 이는 우리가 ‘이전 3일’의 데이터를 사용해 예측했기 때문이다.
실제로 인공지능 모델을 만드는 코드는 model.add(), model.fit() 처럼 단 몇 줄에 불과하다.
더 많은 비중을 차지하는 것은 데이터를 인공지능 모델이 이해할 수 있도록 변환하고, 모델이 출력한 결과를 우리가 이해하기 쉽게 다시 변환하는 ‘데이터 전처리’과정이다.
이처럼 성공적인 인공지능 모델 개발의 성패는 복잡한 알고리즘 뿐만 아니라, 데이터를 얼마나 잘 이해하고 섬세하게 다루느냐에 달려있다고 해도 과언이 아니다.
주황색과 초록색 선이 바로 인공지능이 예측한 확진자 수이고, 파란색 선이 실제 확진자 수이다.
직전 3일치를 바탕으로 다음 날을 예측하기 때문에 처음 3일 동안의 예측값이 없는 것을 확인할 수 있다.
이렇게 인공지능을 만드는 비중은 크지 않다. 비중이 큰 부분은 바로 데이터를 인공지능 모델에 넣을 수 있도록 변환하고, 모델로 나온 데이터를 보기 쉽게 변환하는 부분이다. 이처럼 인공지능 모델을 만들기 위해서는 데이터를 얼마나 잘 처리하느냐가 성패를 좌우한다.
참고 사이트 & 함께 보면 좋은 사이트
본 포스트는 이영호 저자의 모두의 인공지능 with 파이썬을 기반으로 스터디하며 정리한 내용들입니다.
