AI - 숫자 생성 인공지능
in DEV on Ai, Ml, Deep-learning, Python, Keras, Tensorflow, Gan, Mnist, Neural-network, Image-generation, Tutorial, 인공지능, 머신러닝, 딥러닝, 파이썬, 케라스, 이미지생성, 튜토리얼
AI - 숫자 인식 인공지능 만들기 에서 인공지능이 어떻게 이미지를 ‘인식’하고 ‘분류’하는지 알아보았다.
여기서는 한 걸음 더 나아가, 스스로 무언가를 ‘창작’하는 인공지능을 만들어본다.
이 포스트에서는 생성적 적대 신경망(GAN, Generative Adversarial Networks)이라는 딥러닝 기법을 사용하여, 마치 사람이 직접 쓴 것 같은 손글씨 숫자 이미지를 만들어내는 인공지능을 개발해본다.
데이터는 이전과 동일하게 MNIST 데이터셋을 활용한다.
GAN 의 기본 원리를 이해하고, ‘생성자(Generator)’와 ‘판별자(Discriminator)’가 어떻게 서로 경쟁하며 학습하는지 직접 확인해본다.
목차
- 1. 숫자 생성 인공지능 개발 원리
- 2. 개발 환경 셋팅
- 3. 데이터 가져오기
- 4. 생성자 신경망 생성
- 5. 판별자 신경망 생성
- 6. GAN 생성 함수 생성
- 7. 결과 확인 함수 생성
- 8. 생성적 적대 신경망 훈련
- 참고 사이트 & 함께 보면 좋은 사이트
1. 숫자 생성 인공지능 개발 원리
이 포스트의 핵심 기술은 GAN(Generative Adversarial Networks, 생성적 적대 신경망)이다.
GAN 은 2개의 신경망이 서로 경쟁하며 학습하는 독특한 구조를 가진다.
GAN 을 구성하는 두 신경망은 아래와 같다.
- 생성자(Generator)
- 처음에는 의미 없는 노이즈(무작위 데이터)로부터 서툰 가짜 이미지를 만들지만, 학습을 거듭하여 판별자를 속일 수 있을 만큼 정교한 진짜 같은 가짜 이미지를 생성하는 것이 목표
- 판별자(Discriminator)
- 생성자가 만든 가짜 이미지와 실제 MNIST 데이터를 구별해내는 훈련을 받아서 진짜와 가짜를 정확하게 판별하는 것이 목표
이 둘의 학습 과정은 아래와 같은 적대적인 방식으로 진행된다.
- 생성자는 가짜 이미지를 만들어서 판별자에게 보여줌
- 판별자는 그 이미지를 보고 진위 여부를 판별하여 피드백을 줌
- 생성자는 판별자를 속이지 못했다면, 그 피드백을 바탕으로 더 진짜같은 이미지를 만드는 방법을 학습함
- 판별자 역시 생성자가 점점 더 정교한 가짜를 만들어내기 때문에, 진짜와 가짜를 구별하는 능력을 계속해서 발전시킴
이러한 경쟁이 반복되면, 결국 판별자가 더 이상 진짜와 가짜를 구분하기 어려울 정도로 생성자의 이미지 생성 능력은 매우 높아진다.
우리는 이렇게 고도로 훈련된 생성자를 이용하여 새로운 숫자 이미지를 만들어 낼 것이다.
2. 개발 환경 셋팅
from keras.models import Model, Sequential
from keras.layers import Dense, Input, LeakyReLU
from keras.optimizers import Adam
from keras.datasets import mnist
from tqdm import tqdm
import numpy as np
import matplotlib.pyplot as plt
from keras.layers import Dense, Input, LeakyReLU
활성화 함수 중 하나인 LeakyReLU 를 사용하여 모델의 성능을 높인다.
from keras.optimizers import Adam
학습한 모델의 오차를 줄이기 위해 경사 하강법을 사용한다.
이 때 사용하는 옵티마이저는 현재 가장 널리 사용되고 있는 아담(Adam) 옵티마이저를 사용한다.
from tqdm import tqdm
모델 학습을 시각적으로 보여주는 라이브러리인 tqdm 라이브러리를 불러온다.
3. 데이터 가져오기
판별자가 ‘진짜’ 손글씨가 무엇인지 학습하려면 당연히 원본 데이터가 필요하다.
여기서는 잘 알려진 MNIST 손글씨 숫자 데이터셋을 사용한다.
MNIST 데이터셋은 총 6만 개의 훈련 데이터와 1만 개의 검증 데이터로 구성되어 있다.
전체 데이터를 모두 사용하면 학습 시간이 길어질 수 있으므로, 여기서는 1만 개의 검증 데이터만 사용하여 빠르게 개념을 익혀본다.
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 데이터 정규화: 픽셀 값을 -1 ~ 1 범위로 조정
x_test = (x_test.astype(np.float32) - 127.5) / 127.5
# 데이터 형태 변환: (28, 28) 이미지를 784 크기의 1차원 벡터로 변환
mnist_data = x_test.reshape(10000, 784)
print(mnist_data.shape)
# (10000, 784)
데이터 정규화: x_test = (x_test.astype(np.float32)-127.5) / 127.5
MNIST 이미지의 각 픽셀은 0(검은 색)부터 255(흰색)까지의 값을 가진다.
신경망이 보다 안정적으로 학습하기 위해 이 범위를 -1~1 사이로 조정한다.
각 픽셀 값에서 중간값인 127.5를 빼고, 다시 127.5로 나누어주면 0은 -1로, 255는 1로 변환된다.
이 작업은 1. 코로나 19 확진자 수 예측 인공지능 개발 원리 에서 사용한 MinMaxScaler() 와 동일한 목적을 가진다.
데이터 형태 변환: mnist_data = x_test.reshape(10000, 784)
기존의 2차원 이미지(28*28)를 Dense 레이어로 구성된 우리 신경망 모델이 입력받을 수 있도록 1차원 벡터(784개) 형태로 쭉 펼쳐준다.
3. 입력 데이터 전처리(X): 모델에 맞는 형태로 변환에서 한 것처럼 28*28 형태인 데이터를 1열로 나타내기 위해 데이터 형태를 변경해주는 방식과 같다.
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11490434/11490434 ━━━━━━━━━━━━━━━━━━━━ 0s 0us/step
(10000, 784)
# 총 1만개의 데이터가 있으며, 데이터 1개에는 784개의 값이 들어가있음
10000
실행 결과 (10000, 784) 는 총 1만개의 이미지가 각각 784개의 픽셀 값으로 준비되어 있음을 의미한다. 이제 이 데이터를 가지고 GAN 의 두 신경망인 생성자와 판별자를 만들어보자.
4. 생성자 신경망 생성
이제 GAN 의 첫 번째 신경망인 생성자(Generator) 를 만들어보자.
생성자의 역할은 무작위 노이즈를 입력받아서 그럴듯한 숫자 이미지 데이터로 변환하는 것이다. 즉 아무런 의미 없는 데이터에서 의미 있는 창작물을 만들어낸다.
아래 코드는 아직 훈련되지 않은 생성자 모델이다. 이 모델은 앞으로 판별자와의 경쟁을 통해 점차 진짜같은 이미지를 생성하도록 진화할 것이다.
def create_generator():
generator = Sequential()
# 1. 모델의 입력 형태를 정의하는 Input 레이어를 추가합니다.
# 100은 100개의 픽셀을 넣을 거라서 큰 의미는 없으며, 이 100개의 픽셀은 노이즈값으로, 100개의 픽셀값이 랜덤한 값을 가진다.
generator.add(Input(shape=(100,)))
# 첫 번째 은닉층은 256개의 뉴런으로 구성됨
generator.add(Dense(units=256))
# LeakyReLU 함수 모양을 보면 음수값은 특정한 기울기를 보이는데 여기서는 그 기울기값을 0.2로 설정
generator.add(LeakyReLU(0.2))
# 두 번째 은닉층은 512개의 뉴런으로 구성
generator.add(Dense(units=512))
generator.add(LeakyReLU(0.2))
# 출력층의 활성화 함수는 tanh 으로 사용하고, 뉴런 수는 784개
# tanh 은 출력값을 -1~1 사이로 맞춰줌
# 784개인 이유는 MNIST 데이터셋 모습이 바로 28*28 개의 픽셀로 구성되어 있기 때문임
# 1*784 처럼 생성자가 만드는 데이터 모습도 이와 같은 모양인 784개의 픽셀을 나열한 모습으로 나타내야 함
# 추후 이 모양을 다시 28*28 형태로 나타내면 숫자와 같은 모습으로 나타남
generator.add(Dense(units=784, activation='tanh'))
return generator
g = create_generator()
g.summary()
- 입력층
- shape=(100,)
- 100개의 랜덤한 숫자로 이루어진 노이즈 벡터가 모든 창작의 시작점이 됨
- 은닉층 1, 2
- Dense, LeakyReLU
- 입력된 단순한 노이즈를 점차 복잡하고 의미 있는 데이터(이미지 특징)으로 변환하는 핵심 부분임
- 뉴런 수를 256 → 512로 점차 늘려가며 표현력을 키움
- 출력층
- units=784
- 최종 출력물은 784개의 픽셀값으로 구성된다. 이는 학습할 MNIST 이미지가
28*28=784픽셀이기 때문이다. - 생성자는 진짜 데이터와 동일한 가짜를 만들어야 한다.
- 최종 출력물은 784개의 픽셀값으로 구성된다. 이는 학습할 MNIST 이미지가
- activation=’tanh’
- tanh 함수는 결과값을 -1에서 1 사이로 만든다. 앞에서 MNIST 데이터를 동일한 범위로 정규화했었는데, 이처럼 진짜와 가짜 데이터의 형식을 일치시키는 것이 중요하다.
- units=784
Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_3 (Dense) │ (None, 256) │ 25,856 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ leaky_re_lu_2 (LeakyReLU) │ (None, 256) │ 0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_4 (Dense) │ (None, 512) │ 131,584 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ leaky_re_lu_3 (LeakyReLU) │ (None, 512) │ 0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_5 (Dense) │ (None, 784) │ 402,192 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 559,632 (2.13 MB)
Trainable params: 559,632 (2.13 MB)
Non-trainable params: 0 (0.00 B)
- Layer(type): 계층의 종류
- dense (Dense)
- 가장 기본적인 신경망 층이다.
- 이전 층의 모든 뉴런과 다음 층의 모든 뉴런이 서로 연결된 상태를 의미하며, ‘완전 연결 계층’이라고도 부른다.
- leaky_re_lu (LeakyReLU)
- 활성화 함수이다.
- Dense 층을 통과한 신호를 다음 층으로 어떻게 전달할지 결정하는 역할을 한다.
- dense (Dense)
- Output Shape: 데이터의 모양
- 데이터가 각 층을 통과한 후 어떤 모양으로 변하는지 보여준다.
- (None, 256) 에서 None 은 한 번에 여러 개의 데이터를 묶어서 처리할 수 있다는 의미이며, 배치 크기를 나타낸다.
- None 는 ‘없다’는 뜻이 아니라 ‘어떤 숫자들 들어올 수 있는 유연한 공간’이라는 의미이다.
- 신경망 모델을 설계할 때는 이 모델이 나중에 훈련하거나 예측할 때 한 번에 몇 개의 데이터를 처리할지 미리 정해두지 않는다.
- 이처럼 실행 시점에 배치 크기가 유동적으로 변할 수 있기 때문에 모델을 정의하는 단계에서는 이 자리를 None 으로 비워둔다.
- 256, 512, 784는 해당 층을 통과한 데이터가 몇 개의 숫자로 이루어져 있는지를 의미한다.
- Param #: 파라미터 개수
- 파라미터는 모델이 학습 과정에서 스스로 최적화하는 가중치(Weight)와 편향(Bias)의 총개수이며, 이 숫자들이 바로 인공지능이 학습하는 대상이다.
- 25,856: (100 뉴런 *256 뉴런) + 256 편향 = (25,600 가중치) + 256 편향
- 131,584: (256*512) + 512
- 402,192: (512*784) + 784
5. 판별자 신경망 생성
이제 판별자 신경망을 만들 차례이다.
판별자는 생성자가 만든 이미지와 진짜 MNIST 이미지를 보고, 그것이 진짜인지 여부를 구별해내는 것이다.
앞에서 생성자 신경망은 어떤 숫자 이미지를 만들어내는 신경망이고, 여기서 만들 판별자 신경망은 생성자 신경망이 만든 이미지가 가짜인지 정확하게 판별하는 신경망이다. 이 신경망 역시 훈련되지 않은 신경망으로, 앞으로 생성적 적대 신경망(GAN)으로 학습시킬 예정이다.
def create_discriminator():
discriminator = Sequential()
# 784차원의 이미지 벡터(진짜 혹은 가짜)를 입력 받습니다.
생성자가 만든 손글씨(784개의 픽셀로 구성된)를 넣기 때문이다.
discriminator.add(Input(shape=(784,)))
# 첫 번째 은닉층 512개의 뉴런으로 구성되어있다.
discriminator.add(Dense(units=512))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dense(units=256))
discriminator.add(LeakyReLU(0.2))
# 최종 출력값은 1개이다. 판별자가 하는 것은 데이터의 진위 여부를 판단하는 것이다.
# 따라서 진짜면 1, 가짜면 0이라는 숫자를 보여준다.
discriminator.add(Dense(units=1, activation='sigmoid'))
# 모델 컴파일
# !! 여기서 컴파일하면 정상적으로 학습이 되지 않음
# discriminator.compile(loss='binary_crossentropy', optimizer=Adam(learning_rate=0.0002, beta_1=0.5))
return discriminator
d = create_discriminator()
# d.summary()
- 입력층
- shape(784,)
- 판별자는 784개의 픽셀 값으로 이루어진 이미지를 입력받음
- 이 이미지는 실제 MNIST 데이터셋에서 온 ‘진짜’일 수도, 생성자가 방금 만든 ‘가짜’일 수도 있음
- 은닉층 1, 2
- Dense, LeakyReLU
- 생성자와 반대로 입력된 이미지의 복잡한 정보를 점차 압축(512 → 256)하며 진위 여부를 판단하는데 필요한 핵심 특징들을 추출함
- 출력층
- units=1
- 출력은 단 하나의 뉴런
- activation=’sigmoid’
- 시그모이드 함수는 최종 결과값을 0에서 1사이로 만듦
- 이는 ‘진짜일 확률’을 나타냄 (1에 가까우면 ‘진짜’, 0에 가까우면 ‘가짜’)
- units=1
- compile() 설정
- loss=’binary_crossentropy’
- 진짜와 가짜, 둘 중 하나를 맞히는 이진 분류(Binary Classification) 문제이므로 이항 교차 엔트로피(binary_crossentropy) 손실 함수를 사용함
- optimizer=Adam(learning_rate=0.0002, beta_1=0.5)
- GAN 은 훈련 과정이 민감하여 최적화 도구인 옵티마이저의 세부 설정이 중요함
- 여기서 설정한 학습률(learning_rate)과 베타(beta_1)값은 GAN 이 안정적으로 수렴하도록 돕는 값들임
- learning_rate
- 경사 하강법에서 가중치를 한 번에 얼마나 업데이트할 지 결정하는 학습률을 작게 설정하여 신중하게 학습을 진행함
- beta_1
- ‘과거의 학습 방향을 얼마나 기억할 것인가’를 결정하는 값으로 기본값은 0.9임
- 이는 과거의 학습 방향을 90% 정도 신뢰하고, 현재의 방향은 10%만 반영한다는 의미임
- beta_1 이 너무 높으면, 즉 ‘관성’이 너무 크면 판별자가 특정 방향으로 학습을 잘 진행하고 있었는데 그 사이에 생성자가 새로운 전략을 들고 나오면 판별자는 기존의 큰 관성 때문에 재빨리 대응하지 못하고 균형을 잃게 됨. 따라서 여기서는 0.5로 설정함
- loss=’binary_crossentropy’
Model: "sequential_4"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense_6 (Dense) │ (None, 512) │ 401,920 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ leaky_re_lu_4 (LeakyReLU) │ (None, 512) │ 0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_7 (Dense) │ (None, 256) │ 131,328 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ leaky_re_lu_5 (LeakyReLU) │ (None, 256) │ 0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_8 (Dense) │ (None, 1) │ 257 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 533,505 (2.04 MB)
Trainable params: 533,505 (2.04 MB)
Non-trainable params: 0 (0.00 B)
6. GAN 생성 함수 생성
생성자와 판별자를 각각 만들었으니, 이제 생성적 적대 신경망(GAN)으로 이 둘을 하나로 연결해보자.
이 결합된 모델의 핵심 목표는 생성자를 훈련시키는 것이다.
생성자라는 ‘선수’가 진짜같은 그림을 그리면, 판별자라는 코치는 피드백을 준다. 이 과정에서 선수는 성장하지만, 코치 자체의 실력(가중치)는 변하지 않는다.
생성자 신경망과 판별자 신경망을 만들었으니 이제 생성적 적대 신경망(GAN)을 만들 준비가 끝났다. 이제 생성자 신경망과 판별자 신경망을 적절하게 학습시켜 보자.
from keras.models import Model
from keras.layers import Input
# GAN 생성 함수
def create_gan(discriminator, generator):
# 핵심: GAN 모델에서는 판별자가 학습하지 못하도록 가중치를 freeze 함
discriminator.trainable = False
# 생성적 적대 신경망인 gan 에 입력할 데이터 모습을 정함
# 입력하는 값은 100개의 값으로 구성된 데이터이고, 콤마 뒤의 값이 비어있는 이유는 총 데이터의 개수를 넣기 위함임
# 이렇게 값을 비워두면 실제 데이터 개수(여기서는 1만개)를 자동으로 넣어줌
gan_input = Input(shape=(100,))
# 생성자 신경망에 바로 윗줄에서 작성할 픽셀 100개의 값과 데이터의 전체 수(Input(shape=(100,))만큼 데이터를 넣음
# 이 픽셀 100개는 노이즈값으로, x에는 생성자가 노이즈를 입력받아 만든 가짜 이미지들이 저장됨
x = generator(gan_input)
# 생성적 적대 신경망 gan 의 결과값 데이터 정의
# 생성자가 만든 그림(x)을 보고 판별자가 판단한 결과, 판단 결과는 진짜 혹은 가짜 둘 중 하나로 나옴
gan_output = discriminator(x)
# 생성자와 판별자를 연결한 최종 생성적 적대 신경망인 gan 모델 정의
# 입력값은 생성자 신경망이 만든 그림이고, 출력값은 판별자 신경망이 판단한 결과
gan = Model(inputs=gan_input, outputs=gan_output)
# GAN 모델 컴파일
gan.compile(loss='binary_crossentropy', optimizer='adam')
return gan
# !! 판별자를 동결시키고 GAN 모델 컴파일(생성자 훈련용)
d.trainable = False
gan = create_gan(d, g)
gan.summary()
# !! 판별자를 다시 학습 가능하게 만들고, 판별자 모델만 따로 컴파일(판별자 훈련용)
d.trainable = True
d.compile(loss='binary_crossentropy', optimizer=Adam(learning_rate=0.0002, beta_1=0.5))
d.summary()
discriminator.trainable = False
이 부분이 가장 중요하다.
GAN 모델을 훈련시킬 때는 생성자만 학습해야 한다. 만약 여기서 판별자까지 학습하게 되면, 판별자는 생성자가 만든 이미지를 무조건 ‘가짜’라고 판별하도록 학습되어 버려서 생성자에게 올바른 피드백을 줄 수 없다.
따라서 판별자의 가중치를 동결하여 오직 피드백을 주는 ‘코치’의 역할만 하도록 제한한다.
gan = Model(inputs=gan_input, outputs=gan_output)
생성자와 판별자는 순서대로 연결한다.
데이터의 흐름은 노이즈 입력 → 생성자 → 가짜 이미지 → 판별자 → 최종 판별 결과가 된다.
gan.compile(loss=’binary_crossentropy’, optimizer=’adam’)
GAN 의 목표는 생성자가 판별자를 완벽하게 속이는 것이다.
즉, 생성자가 만든 가짜 이미지를 판별자가 ‘진짜(1)’라고 판단하게 만들어야 한다.
따라서 진짜와 가짜, 둘 중 하나를 맞히는 이진 분류(Binary Classification) 문제이므로 이항 교차 엔트로피(binary_crossentropy) 손실 함수를 사용한다.
Model: "functional_20"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ input_layer_6 (InputLayer) │ (None, 100) │ 0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ sequential_2 (Sequential) │ (None, 784) │ 559,632 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ sequential_3 (Sequential) │ (None, 1) │ 533,505 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 1,093,137 (4.17 MB)
Trainable params: 559,632 (2.13 MB)
Non-trainable params: 533,505 (2.04 MB)
- 입력층
- 노이즈값이 100개의 픽셀값에 들어감
- 두 번째 레이어
- 생성자 신경망에서 출력된 값의 모습
- 세 번째 레이어
- 생성자 신경망에서 만든 그림이 진짜인지 가짜인지 판별자가 판단한 결과
- Trainable params: 559,632 (2.13 MB)
- 가장 중요한 부분이다. 학습 가능한 파라미터가 정확히 생성자의 파라미터 수와 일치한다.
- 생성자의 파라미터: 559,632개
- 생성자는 3개의 Dense 층으로 구성되어 있다.
- 1층: (100*256) + 256 = 25,856
- 2층: (256*512) + 512 = 131,584
- 3층: (512*784) + 784 = 402,192
- 판별자의 파라미터: 533,505개
- 판별자 역시 3개의 Dense 층으로 구성되어 있다.
- 1층: (784*512) + 512 = 401,920
- 2층: (512*256) + 256 = 131,328
- 3층: (256*1) + 1 = 257
이 GAN 모델을 학습(gan.fit())시키면, 판별자의 533,505개의 파라미터는 그대로 둔 채 생성자의 559,632개만 업데이트된다.
7. 결과 확인 함수 생성
GAN 의 성능은 단순히 숫자로 된 ‘정확도’로 평가하기 어렵다. 가장 확실한 방법은 생성자가 만들어낸 이미지를 우리 눈으로 직접 보고 얼마나 진짜 같은지 판단하는 것이다.
이번에 만드는 함수는 학습 중간중간 생성자의 현재 실력을 확인하는 ‘중간 점검용’ 역할을 한다.
# 결과 확인 함수
def plot_generated_images(generator):
# 생성자에 넣어줄 노이즈값 생성
noise = np.random.normal(loc=0, scale=1, size=[100,100])
# 노이즈를 생성자 모델에 넣어 100개의 이미지 생성
generated_images = generator.predict(noise)
# 생성된 1차원 이미지(784,)를 2차원(28,28) 형태(그림 형태)로 변환
generated_images = generated_images.reshape(100, 28, 28)
# 10X10 격자에 생성된 이미지 100개를 시각화한다.
plt.figure(figsize=(10, 10))
for i in range(generated_images.shape[0]):
plt.subplot(10, 10, i+1)
plt.imshow(generated_images[i], interpolation='nearest')
# 그림 이름은 넣지 않음
plt.axis('off')
# 지금까지 만든 그림을 화면에 보여줌
plt.tight_layout()
#plt.show() # 이미지를 실제로 표시
noise = np.random.normal(loc=0, scale=1, size=[100,100])
균일한 값을 생성할 수 있도록 넘파이의 랜덤값 생성 라이브러리 중 정규 분포 함수를 이용한다.
첫 번째 0은 평균이 0이라는 의미이고, 두 번째 1은 평균에서 1만큼씩 떨어져있는 값(즉, -1~1 사이의 값)을 의미한다.
-1~1 사이의 값을 생성하는 것은 사용한 MNIST 데이터셋 모습을 -1~1 사이의 값으로 변형했기 때문에 이와 비슷한 형태로 만들어주는 것이다.
세 번째 값은 노이즈 100개를 생성한다.
size=[100,100] 은 100개의 숫자(noise vector)로 이루어진 데이터를 100개(batch_size)개 만든다는 의미이다.
- 첫 번째 100(batch size)
- 한 번에 생성하고 싶은 이미지의 총개수
- 두 번째 100(noise vector dimension)
- 이미지 하나를 만드는 데 필요한 재료의 크기
- 이는 이전에 만든 생성자 모델의 입력 크기(Input(shape=100,))와 정확히 일치해야 함
generated_images = generated_images.reshape(100, 28, 28)
생성자 모델의 최종 출력층을 떠올려보자.
generator.add(Dense(units=784, activation='tanh'))
위 코드처럼 생성자가 최종적으로 784개의 픽셀값으로 이루어진 1차원 벡터를 출력하도록 설계했다. 사람이 보기 좋은 이미지로 만들려면, 이 1차원 데이터를 원래의 2차원 이미지 크기인 28*28 픽셀로 다시 변환(reshape)해줘야 한다.
plt.subplot(10, 10, i+1)
subplot() 함수는 전체 그림판을 여러 개의 작은 칸으로 나누는 역할을 한다.
- 첫 번째 10: 전체 그림판을 10개의 행(row)로 나눔
- 두 번째 10: 전체 그림판을 10개의 열(column)로 나눔
- 세 번째 i+1: 그 중 i+1 번째 칸에 지금부터 그릴 그림을 넣음
plt.imshow(generated_images[i], interpolation=’nearest’)
imshow() 함수는 이미지를 출력한다.
interpolation은 이미지를 출력할 때 각 픽셀을 어떻게 나타낼 지 결정하는 것이다. 즉, 저해상도 이미지를 화면에 표시할 때 픽셀 사이의 색을 어떻게 채워 부드럽게 보여줄 지 결정하는 방법이다.
- nearest (최근접 이웃 보간법)
- 가장 단순하고 빠른 방식
- 각 픽셀의 색을 가장 가까운 실제 데이터의 색으로 그대로 채움
- 결과적으로 흐릿함 없이 각 픽셀이 명확하게 보이는 격자무늬 또는 도트 느낌이 남
- AI 가 만든 순수한 결과물을 왜곡 없이 보고 싶을 때 가장 적합함
- 기타 종류
- bilinear, bicubic 등은 주변 픽셀들의 색을 섞어서 중간 색을 만들어내므로 이미지가 훨씬 부드럽게 보임
- 하지만 원본 데이터가 흐릿하게 뭉개져 보일 수 있음
8. 생성적 적대 신경망 훈련
생성자 신경망과 판별자 신경망을 만들고, 이 둘을 훈련시키기 위한 gan 모델까지 설계했다.
이제 이 두 신경망을 수천 번에 걸쳐 서로 경쟁시키며 점차 발전시키는, GAN 훈련 과정을 보자.
이 훈련 과정은 크게 두 단계로 나뉜다.
- 판별자 훈련
- 생성자 훈련
이 두 단계를 쉴 새 없이 반복하며 서로의 실력을 끌어올리는 것이 바로 GAN 의 학습 원리이다.
# 한 번에 학습할 이미지 개수 (배치 크기)
batch_size = 128
# 총 훈련 반복 횟수 (에포크)
epochs = 5000
# 신경망 학습
# tqdm 은 5000 반복하는데 그 중 몇 번째 반복인지 눈에 잘 보이게 시각화함
for e in tqdm(range(epochs)):
# --- 1단계: 판별자(Discriminator) 훈련 ---
# 1-1. 진짜 이미지와 가짜 이미지 준비
noise = np.random.normal(0, 1, [batch_size, 100])
# 생성자 모델에 노이즈를 입력하여 생성자 신경망이 그림을 그린 후 결과를 generated_images 에 저장
generated_images = g.predict(noise)
# 실제 MNIST 데이터셋(1만개)에서 128개만 랜덤으로 추출(학습할 때마다 다양한 모양의 손글씨를 인공지능이 학습하도록 하기 위함임)
# 첫 번째부터(now=0) MNIST 데이터셋 개수(high=mnist_data.shape[0])까지, 즉 1만 개의 데이터 중에서 배치 사이즈만큼 랜덤으로 추출
image_batch = mnist_data[np.random.randint(low=0, high=mnist_data.shape[0], size=batch_size)]
# 진짜 이미지와 가짜 이미지를 하나로 합침 (총 256개)
# 이 데이터는 총 256개의 데이터로 되어있으며, 각 데이터에는 -1~1 사이의 값이 784개씩 들어있다.
X = np.concatenate([image_batch, generated_images])
# 1-2. 정답 레이블 생성(=판별자에 전달할 결과값 생성)
# 판별자는 이것으로 그림이 진짜인지 가짜인지 확인할 수 있음
# 앞에서 만든 데이터 개수(256개, 진짜와 가짜 각각 128개)만큼 결과값을 256개 만드는 때 이 때 값은 0으로 채움
y_dis = np.zeros(2*batch_size)
# 진짜 이미지(앞쪽 128개)의 정답은 1로, 가짜 이미지(뒤쪽 128개)의 정답은 0으로 설정
y_dis[:batch_size] = 1
# 1-3. 판별자 학습 진행
# 처음에는 판별자가 먼저 학습할 수 있어야 함
# 정답을 보고 학습하여 생성자가 만든 그림과 진짜 그림을 구별할 수 있어야 하기 때문임
d.trainable = True # 판별자의 가중치를 업데이트할 수 있도록 설정
d.train_on_batch(X, y_dis) # 판별자를 학습시킴, 입력값은 X 이고, 출력값은 y_dis 임
# --- 2단계: 생성자(Generator) 훈련 ---
# 2-1. 생성자를 속이기 위한 데이터 준비
noise = np.random.normal(0, 1, [batch_size, 100])
# 생성자의 목표는 판별자가 '진짜(1)'라고 착각하게 만드는 것
y_gen = np.ones(batch_size)
# 2-2. 생성자 학습 진행 (판별자는 동결)
# 판별자가 더 이상 학습할 수 없도록 한다. 판별자는 이제 학습하는 것이 아니라 생성자가 만든 그림이 진짜인지 판별하는 역할만 한다.
d.trainable = False
# gan 에 노이즈를 입력으로 넣고, 출력값으로 모두 다 진짜(y_gen의 값은 1인 상태)를 출력으로 넣어서 학습시킨다.
gan.train_on_batch(noise, y_gen)
# --- 중간 결과 확인 ---
# 첫 번째 에포크와 1000번째, 2000번째.. 일 때 생성자가 만든 그림을 출력함
if e % 1000 == 0:
print(f"Epoch {e}")
plot_generated_images(g)
noise = np.random.normal(0, 1, [batch_size, 100])
가짜 이미지를 만들기 위한 노이즈 생성한다.
첫 번째 0은 평균이 0이라는 의미, 두 번째 1은 평균에서 1만큼씩 떨어져있는 값(즉, -1~1 사이의 값) 생성하라는 의미이다.
세 번째 [batch_size, 100] 은 batch_size 개수만큼 생성하며, 생성한 데이터는 각각 숫자 100개씩 구성되어 있다는 의미이다. 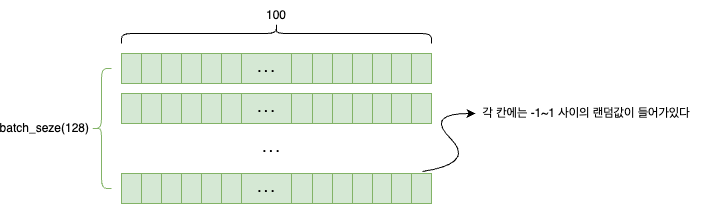
X = np.concatenate([image_batch, generated_images])
이 데이터는 총 256개의 데이터로 되어있으며, 각 데이터에는 -1~1 사이의 값이 784개씩 들어있다.
합쳐진 데이터 X 의 각 데이터에 784개의 값이 들어있는 건 X 를 구성하는 두 재료인 image_batch 와 generated_images 의 형태를 보면 알 수 있다.
- image_batch
- 처음에 MNIST 데이터를 전처리할 때 mnist_data (10000, 784) 형태로 만들었다. 여기서 batch_size 만큼 뽑아도 각 이미지 데이터는 여전히 784개의 픽셀을 가진다.
- generated_images
- 생성자 모델의 최종 출력층이 Dense(784,) 이므로, 생성자가 만든 가짜 이미지 역시 784개의 픽셀값으로 이루어져 있다.
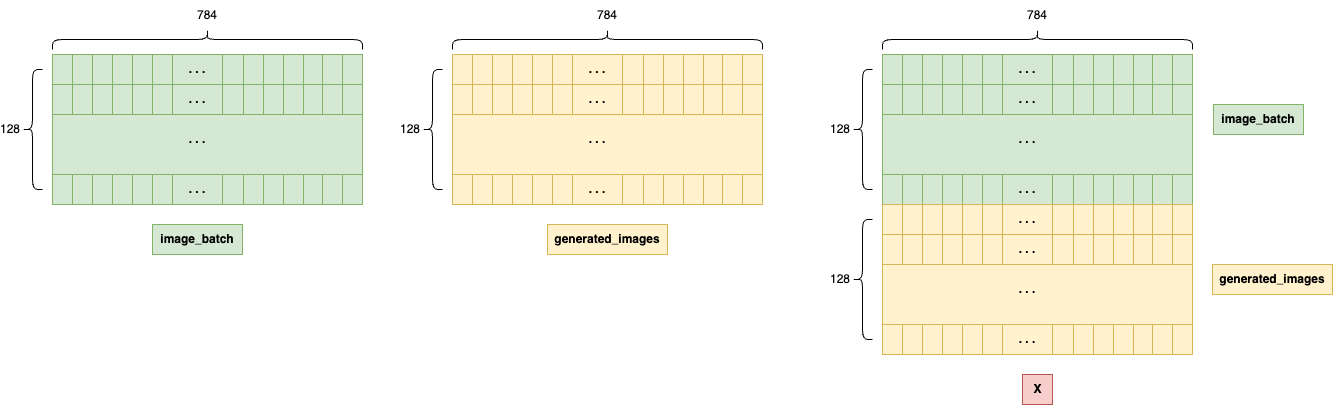
- 생성자 모델의 최종 출력층이 Dense(784,) 이므로, 생성자가 만든 가짜 이미지 역시 784개의 픽셀값으로 이루어져 있다.
y_dis[:batch_size] = 1
각 이미지 데이터는 784개인데 1을 어디에 어떻게 넣어준다는 걸까?
우리는 이미지 데이터(X)에 넣는 것이 아니다. 이미지 데이터(X)와는 별개로 존재하는 정답지인 y_dis를 만드는 것이다.
- X
- 문제지이다.
- 총 256개의 이미지 문제([이미지1, 이미지2, …, 이미지256])가 들어있고, 각 이미지는 784개의 픽셀로 구성된다.
shape: (256, 784)
- y_dis
- 정답지이다.
- 총 256개의 정답([정답1, 정답2, …, 정답256])이 들어있고, 각 정답은 1(진짜) 또는 0(가짜)라는 숫자 하나이다.
shape: (256,)
y_dis[:batch_size] = 1 이 코드는 ‘정답지의 첫 128 칸에 정답을 ‘1’이라고 적어라’라는 뜻이다. 문제지(X)의 첫 128개 문제는 진짜 이미지이기 때문이다.
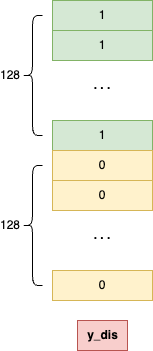
d.train_on_batch(X, y_dis)
판별자에 입력 데이터(X)를 주고 판별자를 통해 나온 출력값과 정답 데이터(y_dis)의 결과값을 비교하여 오차를 줄이는 방식으로 판별자를 학습시킨다.
<훈련 흐름 요약>
- 판별자 Turn
- 진짜 이미지 128개와 생성자가 막 만들어낸 가짜 이미지 128개를 섞어서 판별자에게 보여준다.
- 그리고 “앞에 128개는 진짜고, 뒤에 128개는 가짜야”라고 정답을 알려주며 훈련시킨다. (d.train_on_batch())
- 생성자 Turn
- 판별자의 가중치를 잠그고 ‘평가 모드’로 전환시킨다.
- 생성자는 새로운 가짜 이미지를 만들어 판별자에게 제출하고 “이걸 ‘진짜’라고 판단하도록 스스로를 발전시켜봐”라고 훈련시킨다. (gan.train_on_batch())
이 과정을 수천 번 반복하면, 생성자는 판별자를 속이기 위해 점점 더 진짜 같은 이미지를 만들게 되고, 판별자 또한 속지 않기 위해 점점 더 날카로운 감식안을 갖게 된다.
이 경쟁의 결과로 우리는 진짜와 거의 구분이 불가능한 이미지를 생성하는 AI 를 얻게 된다.
아래 그림을 보면 학습 횟수가 많아질수록 점점 더 손글씨 데이터와 비슷한 모양의 숫자가 만들어지는 것을 확인할 수 있다.





전체 코드
from keras.models import Model, Sequential
from keras.layers import Dense, Input, LeakyReLU
from keras.optimizers import Adam
from keras.datasets import mnist
from tqdm import tqdm
import numpy as np
import matplotlib.pyplot as plt
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 데이터 정규화: 픽셀 값을 -1 ~ 1 범위로 조정
x_test = (x_test.astype(np.float32) - 127.5) / 127.5
# 데이터 형태 변환: (28, 28) 이미지를 784 크기의 1차원 벡터로 변환
mnist_data = x_test.reshape(10000, 784)
print(mnist_data.shape)
len(mnist_data)
def create_generator():
generator = Sequential()
# 1. 모델의 입력 형태를 정의하는 Input 레이어를 추가합니다.
# input_dim=100은 shape=(100,)과 동일합니다.
# 100은 100개의 픽셀을 넣을 거라서 큰 의미는 없으며, 이 100개의 픽셀은 노이즈값으로, 100개의 픽셀값이 랜덤한 값을 가진다.
generator.add(Input(shape=(100,)))
# 첫 번째 은닉층은 256개의 뉴런으로 구성됨
generator.add(Dense(units=256))
# LeakyReLU 함수 모양을 보면 음수값은 특정한 기울기를 보이는데 여기서는 그 기울기값을 0.2로 설정
generator.add(LeakyReLU(0.2))
# 두 번째 은닉층은 512개의 뉴런으로 구성
generator.add(Dense(units=512))
generator.add(LeakyReLU(0.2))
# 출력층의 활성화 함수는 tanh 으로 사용하고, 뉴런 수는 784개
# 784개인 이유는 MNIST 데이터셋 모습이 바로 28*18 개의 픽셀로 구성되어 있기 때문임
# 1*784 처럼 생성자가 만드는 데이터 모습도 이와 같은 모양인 784개의 픽셀을 나열한 모습으로 나타내야 함
# 추후 이 모양을 다시 28*28 형태로 나타내면 숫자와 같은 모습으로 나타남
generator.add(Dense(units=784, activation='tanh'))
return generator
g = create_generator()
g.summary()
def create_discriminator():
discriminator = Sequential()
# 이 모델에 입력하는 값은 784이다. 생성자가 만든 손글씨(784개의 픽셀로 구성된)를 넣기 때문이다.
discriminator.add(Input(shape=(784,)))
# 첫 번재 은닉층 512개의 뉴런으로 구성되어있다.
discriminator.add(Dense(units=512))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dense(units=256))
discriminator.add(LeakyReLU(0.2))
# 최종 출력값은 1개이다. 판별자가 하는 것은 데이터의 진위 여부를 판단하는 것이다.
# 따라서 진짜면 1, 가짜면 0이라는 숫자를 보여준다.
discriminator.add(Dense(units=1, activation='sigmoid'))
# !!컴파일
#discriminator.compile(loss='binary_crossentropy', optimizer=Adam(learning_rate=0.0002, beta_1=0.5))
return discriminator
d = create_discriminator()
#d.summary()
# GAN 생성 함수
def create_gan(discriminator, generator):
# 판별자가 학습하지 못하도록 막음
discriminator.trainable = False
# 생성적 적대 신경망인 gan 에 입력할 데이터 모습을 정함
# 입력하는 값은 100개의 값으로 구성된 데이터이고, 콤마 뒤의 값이 비어있는 이유는 총 데이터의 개수를 넣기 위함임
# 이렇게 값을 비워두면 실제 데이터 개수(여기서는 1만개)를 자동으로 넣어줌
gan_input = Input(shape=(100,))
# 생성자 신경망에 바로 윗줄에서 작성할 픽셀 100개의 값과 데이터의 전체 수(Input(shape=(100,))만큼 데이터를 넣음
# 이 픽셀 100개는 노이즈값임
# x에는 생성자가 만든 새로운 그림들이 저장됨
x = generator(gan_input)
# 생성적 적대 신경망 gan 의 결과값 데이터 정의
# 생성자가 만든 그림(x)을 보고 판별자가 판단한 결과, 판단 결과는 진짜 혹은 가짜 둘 중 하나로 나옴
gan_output = discriminator(x)
# 생성적 적대 신경망인 gan 모델 설계
# 입력값은 생성자 신경망이 만든 그림이고, 출력값은 판별자 신경망이 판단한 결과
gan = Model(inputs=gan_input, outputs=gan_output)
# 신경망의 오차값을 줄이는 방법
gan.compile(loss='binary_crossentropy', optimizer='adam')
return gan
# !! 판별자를 동결시키고 GAN 모델 컴파일(생성자 훈련용)
d.trainable = False
gan = create_gan(d, g)
gan.summary()
# !! 판별자를 다시 학습 가능하게 만들고, 판별자 모델만 따로 컴파일(판별자 훈련용)
d.trainable = True
d.compile(loss='binary_crossentropy', optimizer=Adam(learning_rate=0.0002, beta_1=0.5))
d.summary()
# 결과 확인 함수
def plot_generated_images(generator):
# 생성자에 넣어줄 노이즈값 생성
# 이 때 균일한 값을 생성할 수 있도록 넘파이의 랜덤값 생성 라이브러리 중 정규 분포 함수 이용
# 첫 번째 0은 평균이 0이라는 의미이고,
# 두 번째 1은 평균에서 1만큼씩 떨어져있는 값(즉, -1~1사이의 값)
# 세 번째 값은 노이즈 100개를 생성한다.
# 각각의 노이즈는 숫자 100개씩 구성되어 있다는 것으로, 이 함수를 호출할 때마다 100개의 그림을 그려달라는 의미임
noise = np.random.normal(loc=0, scale=1, size=[100,100])
# generator 도 신경망 모델이므로 predict() 함수 이용 가능
# 위의 노이즈를 신경망에 넣어서 값을 예측하는 기능
generated_images = generator.predict(noise)
# 이 형태를 그림 형태로 바꾸어준다.
generated_images = generated_images.reshape(100, 28, 28)
# 그림 크기를 정한다.
plt.figure(figsize=(10, 10))
# 100개의 그림을 그려준다.
for i in range(generated_images.shape[0]):
# 그림 위치를 정한다. ??? 각각의 인자값이 의미하는 거
plt.subplot(10, 10, i+1)
# imshow() 함수는 이미지를 출력함
plt.imshow(generated_images[i], interpolation='nearest')
# 그림 이름은 넣지 않음
plt.axis('off')
# 지금까지 만든 그림을 화면에 보여줌
plt.tight_layout()
plt.show()
# 한 번에 학습할 이미지 개수 (배치 크기)
batch_size = 128
# 총 훈련 반복 횟수 (에포크)
epochs = 5000
# 신경망 학습
# tqdm 은 5000 반복하는데 그 중 몇 번째 반복인지 눈에 잘 보이게 시각화함
# 신경망 학습
for e in tqdm(range(epochs)):
# --- 1단계: 판별자(Discriminator) 훈련 ---
# 1-1. 진짜 이미지와 가짜 이미지 준비
noise = np.random.normal(0, 1, [batch_size, 100])
generated_images = g.predict(noise)
image_batch = mnist_data[np.random.randint(low=0, high=mnist_data.shape[0], size=batch_size)]
X = np.concatenate([image_batch, generated_images])
y_dis = np.zeros(2 * batch_size)
y_dis[:batch_size] = 1
# 1-2. 판별자 학습 진행
# 판별자를 훈련시키기 직전에 학습 가능하도록 설정합니다.
d.trainable = True
d.train_on_batch(X, y_dis)
# --- 2단계: 생성자(Generator) 훈련 ---
# 2-1. 생성자를 속이기 위한 데이터 준비
noise = np.random.normal(0, 1, [batch_size, 100])
y_gen = np.ones(batch_size)
# 2-2. 생성자 학습 진행
# 생성자를 훈련시킬 때는 판별자의 가중치가 변하면 안 되므로 동결합니다.
d.trainable = False
gan.train_on_batch(noise, y_gen)
# --- 중간 결과 확인 ---
if e % 1000 == 0:
print(f"Epoch {e}")
plot_generated_images(g)
참고 사이트 & 함께 보면 좋은 사이트
본 포스트는 이영호 저자의 모두의 인공지능 with 파이썬을 기반으로 스터디하며 정리한 내용들입니다.
